Логіка
ЛО́ГІКА (від грец. λογιχή — проза, слово, розповідь, значення і смисл, розум, число, пропорція, причина, розумна основа) — наука про принципи і правила, яких необхідно дотримуватися; дослідження міркувань для створення теорії їхньої правильності. Проте мислення як складний феномен є обʼєктом вивчення не лише Л., а й багатьох ін. наук — гносеології, психології, кібернетики тощо. У центрі уваги Л. — форми і закони мислення заг.-люд. характеру, що виявляються в побудові правил. схем, стандартів, канонів міркувань, завжди істин. формул. Як самост. наука Л. виникла у 4 ст. до н. е. Її засн. вважають давньогрец. філософа Аристотеля. У праці «Όργανον» («Органон») він сформулював т. зв. осн. закони Л. (три з чотирьох — закон тотожності, закон суперечності і закон виключеного третього), дослідив поняття й судження, створив теорію дедуктив. умовиводів, насамперед вчення про простий категорич. силогізм. До Аристотеля над проблемами Л. працювали давньогрец. філософи Парменід Елейський, Платон та ін. Пізніше Л. Аристотеля збагачено працями давньогрец. мислителів Теофраста, Хрисіппа, візантійця М. Псьола. У наш час створ. багато логіч. систем, виявити в них істотні ознаки, характерні для кожної з них, надзвичайно важко, а на думку багатьох фахівців із Л., навіть неможливо. Вдаючись до різних основ поділу, розрізняють Л.: традиційну і нетрадиційну (сучасну); формальну та неформальну; двозначну і багатозначну; модальну та немодальну тощо. Сучасну (символічну) Л. поділяють на класичну і некласичну. Традиц. Л. є першим етапом у розвитку формал. Л. («арифметикою Л.», на відміну від 2-го етапу, який умовно називають «алгеброю Л.»), що розпочався у 4 ст. до н. е. і завершився наприкінці 19 — на поч. 20 ст. (тоді сформувалася сучасна Л.). Традиц. Л. як наука вичерпала потенціал, проте як навч. дисципліна залишається необхідною. Традиц. Л. вивчає «правильне» мислення. Про того, хто не дотримується певних принципів і правил, кажуть, що він мислить нелогічно. Викладаючи традиц. Л., демонструють застосування принципів і правил на прикладах природ. (нац.) мови. При цьому лише частково абстрагуються від змісту думок, тобто вона не є суворо формалізованою (напр., у ній можна виявити помилку «почетверіння термінів»). Традиц. Л. є двозначною (бівалентною), оскільки надає думкам лише два логіч. значення, тобто розглядає їх як істинні або хибні (від ін. логіч. значень, скажімо «невизначено», ця Л. абстрагується). Така Л. звернена до буден. свідомості, оскільки узгоджується зі здоровим глуздом (це не завжди стосується сучас. Л.). Через «обтяженість» природ. мови, яка, виконуючи багато функцій (не тільки засобу передачі теор. знань, а й вираження образів, ставлень і почуттів), традиц. Л. не є бездоганною, бо не усуває невизначеності, двозначності, багатозначності. Сучасна Л. зумовлена потребою подолати вади традиц. Л. (правда, існують ін. причини виникнення сучас. Л., особливо некласичної). Традиц. Л. поділяють на дедуктивну, індуктивну і традуктивну. Дедуктивна Л. досліджує умовиводи, в яких знання рухаються від більш загального до менш загального або часткового чи й одиничного; індуктивна досліджує умовиводи, в яких знання рухаються від одиничного (фактів, виражених одинич. судженнями) до часткового чи й загального; традуктивна — умовиводи, в яких засновки і висновок є судженнями однакового ступеня загальності (одним із видів традукції є аналогія). Творець дедуктив. Л. — Аристотель, осн. заслугою якого є вчення про один із найпоширеніших видів дедуктив. умовиводів — простий категорич. силогізм (умовивід, у якому встановлюється звʼязок між край. термінами у висновку на підставі їхнього відношення до серед. терміна у засновках). Так, у силогізмі «Усі метали електропровідні, ртуть — метал; отже, ртуть електропровідна» звʼязок між поняттями «ртуть» і «електропровідні» (крайні терміни) встановлюється на тій підставі, що й «електропровідні», і «ртуть» перебувають у звʼязку з поняттям «метали» (серед. термін). Зазначимо, що правильність міркування за схемою простого категорич. силогізму уточнюється, конкретизується з допомогою відповід. правил щодо термінів і засновків та правил фігур силогізму (фігура силогізму залежить від місця розташування серед. терміна), дотримання яких дає можливість забезпечити правильність міркувань. Знання названих правил дає можливість користуватися виявленими традиц. Л. правил. схемами побудови міркувань, модусами (ААА¹, ЕАЕ, АІІ, ЕІО, ААІ, ЕАО — за першою фігурою силогізму; ЕАЕ, АОО, АЕЕ, ЕІО, ЕАО, АЕО — за другою; ОАО, ААІ, АІІ, ІАІ, ЕАО, ЕІО — за третьою; ААІ, ЕАО, ІАІ, ЕІО, АЕЕ, АЕО — за четвертою) та відрізняти їх від неправил. (їх 232). До дедуктив. умовиводів належать не тільки прості категоричні силогізми (і скорочені та складні й складноскорочені), а й ін. види умовиводів — розділові (суто розділові, розділово-категоричні, розділово-умовні); умовні (суто умовні, умовно-категоричні, умовно-розділові), які теж необхідно будувати згідно з відповід. правилами. Так, схема умовно-категорич. умовиводу «Якщо А, то В; відомо, що не-В; отже, не-А» є правильною, а схема цього виду умовиводу «Якщо А, то В; не-А; отже, не-В» є неправильною, бо відсутність наслідку свідчить про відсутність причини, а відсутність причини (саме цієї причини — А) не свідчить про відсутність наслідку, оскільки він (наслідок В) міг виникнути в результаті дії ін. причини. Існує думка, ніби висновок, одержаний за схемою дедуктив. умовиводу, не містить у собі ніякої нової інформації, якої б не було у засновках. Проте формал. Л. і не претендує на одержання принципово нових знань. Її завданням є одержання т. зв. вивідного знання. Якщо людство виведе всю інформацію, яка потенційно міститься у відомих йому знаннях, зробить їх явними, то збільшення знань буде колосальним. Індуктивна Л. вивчає умовиводи, в яких знання рухаються від одиничного до загального (деякі логіки вважають індуктивними й умовиводи, в яких висновок одержують із часткових засновків). Значну роль у дослідж. цих умовиводів відіграли, крім Аристотеля, англ. філософи Ф. Бекон (2-а пол. 16 — 1-а чв. 17 ст.) та Дж.-С. Мілль (19 ст.). Перевагою дедукції є те, що вона вдається до заг. положень, в яких акумулюються здобутки науки, а перевагою індукції — використання нею наявного фактич. стану. Недолік дедукції — можливість відриву від реал. стану речей (серед узагальнень науки завжди були і є положення хибні чи, принаймні, недостовірні; відомо, що наука постійно уточнює свої положення, а іноді й відмовляється від деяких з них як недостовірних або і явно хибних). Вихід один — взаємна перевірка і взаємне доповнення дедукції індукцією і навпаки. Важливими в системі традиц. Л. є аналогія, умовивід, в якому на підставі подібності двох предметів в одних властивостях роблять висновок про їх подібність і в ін. властивостях. Яскравим прикладом аналогії є висновок про природу блискавки на основі її порівняння з іскрою, зроблений амер. вченим, політ. діячем 19 ст. Б. Франкліном. Результати, одержані засобами традиц. Л., містяться в сучас. Л. у «знятому» вигляді. Проте проголошення традиц. Л. «першим ступенем» розвитку формал. Л., «арифметикою» не дає підстав для її недооцінювання, а тим більше нехтування. Як алгебра ніколи не витіснить арифметику, так і сучасна (символічна) Л. не здатна позбавити живучості теорії, результатами якої людство послуговувалося протягом тисячоліть. Оскільки ж міркування людей у багатьох сферах життя залишаються «обтяженими» природ. мовою, то без традиц. Л. як навч. дисципліни не обійтися.
Сучасна Л. — ниніш. етап розвитку формал. Л., який розпочався у 2-й пол. 19 — на поч. 20 ст. Сучасна Л. прагне максимально формалізувати думки й міркування (правда, повна формалізація неможлива; про це свідчать доведені 1931 теореми австр. логіка і математика К. Ґьоделя). Завдяки довершеним засобам формалізації сучас. Л. вдалося розширити можливості формал. Л., піддати аналізу нові види міркувань, які перебували поза увагою традиц. Л. Сучасну Л. називають то математичною (її методи подібні до математичних), то символічною (використовує штучну, формалізовану мову, спеціально створ. для логіч. аналізу, — мову символів). До складу класич. Л. входять Л. висловлювань (класична) і Л. предикатів. Л. висловлювань (класична), або пропозиційна, — розділ сучас. Л., що вивчає дескриптивні висловлювання та відношення між ними у структурі міркувань. Вона є найпростішим і водночас фундам. розділом не тільки класич., а й усієї сучас. формал. Л., в певному розумінні навіть зразком для побудови ін. формал. логіч. систем. Л. висловлювань вдається до довершеної (хоч і не універсальної) штуч. мови, завдяки якій здійснює аналіз логіч. структури складних висловлювань. Мову Л. висловлювань характеризують її алфавіт (список знакових засобів, які застосовують у логіч. теорії) і визначення формули. У пропозиц. Л. питання про логічне значення складних висловлювань ставиться й вирішується на основі вивчення їхнього способу побудови з простих висловлювань за допомогою логіч. звʼязок. Простим називається висловлювання, до якого не включають ін. самост. висловлювання (у протилеж. випадку воно буде складним). У цій Л. абстрагуються не лише від змісту простих висловлювань, а й від їхньої субʼєктно-предикат. структури. Висловлювання з однаковим логіч. значенням фактично ототожнюють. Такий підхід має недоліки, проте завдяки цьому Л. висловлювань дозволяє акцентувати увагу на звʼязках між висловлюваннями, схемах побудови правил. міркувань. Л. предикатів (функціонал. Л., кванторна Л., теорія квантифікації) — розділ сучас. класич. Л., у якому аналізують міркування з урахуванням внутр., тобто субʼєктно-предикат. будови простих висловлювань. Л. предикатів зумовлена тією обставиною, що правильність чи неправильність міркування часто залежать не лише від характеру звʼязку між простими висловлюваннями, які входять до його складу, а й від їхньої внутр. структури. Л. висловлювань, абстрагуючись від внутр. будови простих висловлювань, не може пояснити правильність чи неправильність простих міркувань, скажімо, тих, що здійснюються у формі простого категорич. силогізму. Виникла необхідність переборення обмеженості виражал. засобів Л. висловлювань. Л. предикатів розглядають як розширений варіант Л. висловлювань, оскільки вона при побудові міркувань зберігає виражал. засоби Л. висловлювань, всі закони Л. висловлювань є законами Л. предикатів (але не навпаки) тощо. Л. предикатів, як і Л. висловлювань, досліджує дескриптивні висловлювання та їх поєднання в складні; вона теж двозначна; до уваги в ній беруть лише предметні значення мовних виразів, а від їхнього смислового значення абстрагуються. Мова Л. предикатів, крім символів Л. висловлювань, включає: 1) логічні оператори 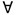 («для кожного») і Ǝ («для деяких», «існує»), які називають квантором загальності і квантором існування; 2) предметні (індивідні) константи — a, b, c, ..., a¹, b¹, c¹, ..., a², b², c², ... — одиничні імена предметів, як правило, власні імена; предметні (індивідні) змінні, призначені для позначення заг. імен природ. мови — x, y, z, ..., x¹, y¹, z¹, ..., x², y², z², ..., ; предикатні змінні — P, Q, R, ..., P¹, Q¹, R¹, ..., P², Q², R², ..., що виражають властивості і відношення обʼєктів. Індивідні змінні набувають значення в довіл. (непорож.) предмет. сфері. Крім них, змінними можуть виступати індивідні константи, або власні імена. Позначені засобами Л. предикатів вирази читають так: (
(«для кожного») і Ǝ («для деяких», «існує»), які називають квантором загальності і квантором існування; 2) предметні (індивідні) константи — a, b, c, ..., a¹, b¹, c¹, ..., a², b², c², ... — одиничні імена предметів, як правило, власні імена; предметні (індивідні) змінні, призначені для позначення заг. імен природ. мови — x, y, z, ..., x¹, y¹, z¹, ..., x², y², z², ..., ; предикатні змінні — P, Q, R, ..., P¹, Q¹, R¹, ..., P², Q², R², ..., що виражають властивості і відношення обʼєктів. Індивідні змінні набувають значення в довіл. (непорож.) предмет. сфері. Крім них, змінними можуть виступати індивідні константи, або власні імена. Позначені засобами Л. предикатів вирази читають так: (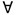 х) Р(х) — «будь-який x має властивість Р»; (Ǝ х) Р(х) — «деякі х мають властивість Р». Індивідну змінну, яка входить до сфери дії квантора по цій змінній, називають звʼязаною; змінну, яка не належить до звʼязаних, називають вільною. В обох наведених формулах змінна x є звʼязаною. Варто зазначити, що справж. змінною є лише вільна змінна, оскільки замість неї можна підставити одне з її значень і одержати осмислений вираз. Звʼязані змінні називають фіктивними. Певне світло на зміст і обсяг поняття «некласич. Л.» міг би пролити логіч. поділ цього поняття, наук. класифікація. Проте такої класифікації не існує. Логіки змушені вдаватися до такого переліку логіч. систем некласич. Л., в якому порушують всі правила логіч. поділу понять. У цих умовах використовують штучну класифікацію, основою якої є місце тієї літери, з якої починається назва різновиду некласич. Л., в укр. азбуці: алетична Л., аксіоматична Л. (Л. оцінок), багатозначна Л., деонтична Л. (Л. норм), епістемічна Л., індуктивно-ймовірнісна Л., інтуїціоніст. Л., когнітивна Л., модальна Л., релевантна Л., паранесуперечлива Л., праксеолог. Л., пресупозиц. Л., темпорал. Л. (часова Л.) тощо. Осмислюючи специфіку тієї чи ін. логіч. системи, необхідно перш за все ознайомитися з її мовою (алфавітом та правильно побудов. формулами), типовими термінами, які входять до структури висловлювань, які досліджуються цією системою тощо. Продемонструємо це на прикладі алетич. Л. Алетична Л. — модал. логічна система, що досліджує висловлювання, до складу яких входять модальності «необхідно», «можливо», «випадково» та відношення цих висловлювань у структурі міркувань. Щоб утворити мову алетич. Л., до мови класич. пропозиц. Л. додають знаки алетич. модальностей: □ — «необхідно», ◊ — «можливо»,
х) Р(х) — «будь-який x має властивість Р»; (Ǝ х) Р(х) — «деякі х мають властивість Р». Індивідну змінну, яка входить до сфери дії квантора по цій змінній, називають звʼязаною; змінну, яка не належить до звʼязаних, називають вільною. В обох наведених формулах змінна x є звʼязаною. Варто зазначити, що справж. змінною є лише вільна змінна, оскільки замість неї можна підставити одне з її значень і одержати осмислений вираз. Звʼязані змінні називають фіктивними. Певне світло на зміст і обсяг поняття «некласич. Л.» міг би пролити логіч. поділ цього поняття, наук. класифікація. Проте такої класифікації не існує. Логіки змушені вдаватися до такого переліку логіч. систем некласич. Л., в якому порушують всі правила логіч. поділу понять. У цих умовах використовують штучну класифікацію, основою якої є місце тієї літери, з якої починається назва різновиду некласич. Л., в укр. азбуці: алетична Л., аксіоматична Л. (Л. оцінок), багатозначна Л., деонтична Л. (Л. норм), епістемічна Л., індуктивно-ймовірнісна Л., інтуїціоніст. Л., когнітивна Л., модальна Л., релевантна Л., паранесуперечлива Л., праксеолог. Л., пресупозиц. Л., темпорал. Л. (часова Л.) тощо. Осмислюючи специфіку тієї чи ін. логіч. системи, необхідно перш за все ознайомитися з її мовою (алфавітом та правильно побудов. формулами), типовими термінами, які входять до структури висловлювань, які досліджуються цією системою тощо. Продемонструємо це на прикладі алетич. Л. Алетична Л. — модал. логічна система, що досліджує висловлювання, до складу яких входять модальності «необхідно», «можливо», «випадково» та відношення цих висловлювань у структурі міркувань. Щоб утворити мову алетич. Л., до мови класич. пропозиц. Л. додають знаки алетич. модальностей: □ — «необхідно», ◊ — «можливо», — «випадково». Відповідні доповнення вносяться й у визначення формули алетич. Л. Необхідність, можливість і випадковість поділяють на логічні і фізичні, чітко їх розмежовуючи. Чи не найлегшим способом розрізнення логіч. систем є ознайомлення з типовими термінами, що входять до структури висловлювань, які досліджує дана система. Якщо для алетич. Л. характерні терміни «необхідно», «можливо», «випадково», то для аксіологічної — «добре», «погано», «байдуже», «краще», «гірше»; для деонтичної — «дозволено», «заборонено», «обовʼязково», «байдуже»; для епістемічної — «вважає» («переконаний»), «сумнівається», «заперечує», «знає», «доказово», «нерозвʼязно», «спростовно»; для темпоральної — «було», «буде», «завжди було», «завжди буде» та ін. Багатозначна (точніше — n>2-значна) Л. — сукупність систем некласич. Л., що керуються принципом, згідно з яким висловлюванням надають більше, ніж два логіч. (істиннісних) значень. Якщо в двознач. Л. висловлюванням надаються лише два логічні значення, або «істина», або «хиба», то в багатознач. допускають й ін. значення (напр., в алетичній — «можливо», «необхідно», «випадково»). Універсальність принципу двозначності вже давно піддавали сумніву. Ще Аристотель стверджував, що висловлювання про майбутні випадкові події, настання яких залежать від волі людини, не належать ні до істинних, ні до хибних. Вони не підкоряються принципу двозначності, оскільки майбутнє певною мірою вільне для зміни і вибору. Пізніше принцип двозначності неодноразово піддавався сумніву. При цьому використовували все нові аргументи, зокрема зазначали, що цей принцип утруднює аналіз деяких висловлювань, насамперед про майбутні події; про нестійкі, перехідні стани явищ; про обʼєкти, недоступні спостереженню; про неіснуючі обʼєкти тощо. Ідеї багатознач. Л. проголошували і логіки давньогрец. мегар. школи (зокрема Діодор Кронос), нім. мислитель 2-ї пол. 17 — поч. 18 ст. Ґ.-В. Ляйбніц, рос. логік і етик 2-ї пол. 20 ст. М. Васильєв. Багатозначна Л. не заперечує і не дискредитує двозначну, а допомагає ясніше осмислити ідеї, на яких ґрунтується двозначна Л., і є в певному розумінні її узагальненням. Перші багатозначні Л. побудували незалежно один від одного представник львів.–варшав. школи Я.-Л. Лукасевич 1920 й амер. математик і логік Е.-Л. Пост 1921. Нині існує немало багатознач. Л., які називають іменами їхніх творців: тризначна і чотиризначна Я.-Л. Лукасевича; n-значна Е.-Л. Поста; тризначні голланд. філософів і математиків Л.-Е.-Я. Брауера й А. Гейтінґа, рос. науковців Д. Бочвара, В. Шестакова тощо. Модал. Л. — розділ некласич. Л., що аналізує логічні звʼязки між висловлюваннями, які конкретизуються відповід. оцінками, даними з тієї чи ін. точки зору. Вона охоплює кілька напрямів, кожен з яких досліджує модал. висловлювання відповід. типу. Загалом вона зосереджується насамперед на таких її різновидах: алетична Л., деонтична Л., епістемічна Л., темпорал. Л. тощо. Заг. властивості модал. Л.: 1) поняття-оцінки, що входять до різних типів модал. висловлювань, взаємно визначаються (мабуть, якоюсь мірою подібно до взаємовизначуваності причини і наслідку, явища і сутності тощо), до того ж за аналогіч. схемою. Нерозвʼязним є те, що одночасно є і недоказовим, і неспростовним; щось є можливим, якщо протилежне не є необхідним; дозволено те, протилежне чому не є обовʼязковим; випадковим є те, що не є ні необхідним, ні неможливим; байдужим є те, що не є ні обовʼязковим, ні забороненим; 2) у кожному різновиді модал. Л. є своя версія принципу модал. повноти (що є модал. аналогом закону виключеного третього), згідно з яким кожне висловлювання є доказовим, спростовним, нерозвʼязним, необхідним, випадковим або неможливим; 3) у кожному різновиді модал. Л. є своя версія принципу модал. несуперечності: висловлювання не може бути одночасно доказовим і спростовним, необхідним і неможливим; 4) модал. поняття різновидів модал. Л. різняться за змістом, проте вони виконують одну й ту ж функцію: уточнюють, конкретизують висловлювання. Правила їхнього використання визначає тільки ця функція, вони не залежать від змісту висловлювань. Саме тому ці правила є спільними для всіх різновидів модал. Л. і мають формал. характер. У наш час модал. Л. бурхливо розвивається, виявляючи все нові модал. оцінки і закріплюючи їх за відповід. термінами; постійно вдосконалюються способи її обґрунтування.
— «випадково». Відповідні доповнення вносяться й у визначення формули алетич. Л. Необхідність, можливість і випадковість поділяють на логічні і фізичні, чітко їх розмежовуючи. Чи не найлегшим способом розрізнення логіч. систем є ознайомлення з типовими термінами, що входять до структури висловлювань, які досліджує дана система. Якщо для алетич. Л. характерні терміни «необхідно», «можливо», «випадково», то для аксіологічної — «добре», «погано», «байдуже», «краще», «гірше»; для деонтичної — «дозволено», «заборонено», «обовʼязково», «байдуже»; для епістемічної — «вважає» («переконаний»), «сумнівається», «заперечує», «знає», «доказово», «нерозвʼязно», «спростовно»; для темпоральної — «було», «буде», «завжди було», «завжди буде» та ін. Багатозначна (точніше — n>2-значна) Л. — сукупність систем некласич. Л., що керуються принципом, згідно з яким висловлюванням надають більше, ніж два логіч. (істиннісних) значень. Якщо в двознач. Л. висловлюванням надаються лише два логічні значення, або «істина», або «хиба», то в багатознач. допускають й ін. значення (напр., в алетичній — «можливо», «необхідно», «випадково»). Універсальність принципу двозначності вже давно піддавали сумніву. Ще Аристотель стверджував, що висловлювання про майбутні випадкові події, настання яких залежать від волі людини, не належать ні до істинних, ні до хибних. Вони не підкоряються принципу двозначності, оскільки майбутнє певною мірою вільне для зміни і вибору. Пізніше принцип двозначності неодноразово піддавався сумніву. При цьому використовували все нові аргументи, зокрема зазначали, що цей принцип утруднює аналіз деяких висловлювань, насамперед про майбутні події; про нестійкі, перехідні стани явищ; про обʼєкти, недоступні спостереженню; про неіснуючі обʼєкти тощо. Ідеї багатознач. Л. проголошували і логіки давньогрец. мегар. школи (зокрема Діодор Кронос), нім. мислитель 2-ї пол. 17 — поч. 18 ст. Ґ.-В. Ляйбніц, рос. логік і етик 2-ї пол. 20 ст. М. Васильєв. Багатозначна Л. не заперечує і не дискредитує двозначну, а допомагає ясніше осмислити ідеї, на яких ґрунтується двозначна Л., і є в певному розумінні її узагальненням. Перші багатозначні Л. побудували незалежно один від одного представник львів.–варшав. школи Я.-Л. Лукасевич 1920 й амер. математик і логік Е.-Л. Пост 1921. Нині існує немало багатознач. Л., які називають іменами їхніх творців: тризначна і чотиризначна Я.-Л. Лукасевича; n-значна Е.-Л. Поста; тризначні голланд. філософів і математиків Л.-Е.-Я. Брауера й А. Гейтінґа, рос. науковців Д. Бочвара, В. Шестакова тощо. Модал. Л. — розділ некласич. Л., що аналізує логічні звʼязки між висловлюваннями, які конкретизуються відповід. оцінками, даними з тієї чи ін. точки зору. Вона охоплює кілька напрямів, кожен з яких досліджує модал. висловлювання відповід. типу. Загалом вона зосереджується насамперед на таких її різновидах: алетична Л., деонтична Л., епістемічна Л., темпорал. Л. тощо. Заг. властивості модал. Л.: 1) поняття-оцінки, що входять до різних типів модал. висловлювань, взаємно визначаються (мабуть, якоюсь мірою подібно до взаємовизначуваності причини і наслідку, явища і сутності тощо), до того ж за аналогіч. схемою. Нерозвʼязним є те, що одночасно є і недоказовим, і неспростовним; щось є можливим, якщо протилежне не є необхідним; дозволено те, протилежне чому не є обовʼязковим; випадковим є те, що не є ні необхідним, ні неможливим; байдужим є те, що не є ні обовʼязковим, ні забороненим; 2) у кожному різновиді модал. Л. є своя версія принципу модал. повноти (що є модал. аналогом закону виключеного третього), згідно з яким кожне висловлювання є доказовим, спростовним, нерозвʼязним, необхідним, випадковим або неможливим; 3) у кожному різновиді модал. Л. є своя версія принципу модал. несуперечності: висловлювання не може бути одночасно доказовим і спростовним, необхідним і неможливим; 4) модал. поняття різновидів модал. Л. різняться за змістом, проте вони виконують одну й ту ж функцію: уточнюють, конкретизують висловлювання. Правила їхнього використання визначає тільки ця функція, вони не залежать від змісту висловлювань. Саме тому ці правила є спільними для всіх різновидів модал. Л. і мають формал. характер. У наш час модал. Л. бурхливо розвивається, виявляючи все нові модал. оцінки і закріплюючи їх за відповід. термінами; постійно вдосконалюються способи її обґрунтування.