Матриць теорія

Визначення і загальна характеристика

МА́ТРИЦЬ ТЕО́РІЯ — роз­діл математики, що ви­вчає властивості та за­стосува­н­ня матриць. Матриці мають довготривалу історію. У класич. тв. «Математика в девʼяти книгах», написаному до н. е. у Китаї, вміщені приклади викори­ста­н­ня т. зв. чарів. квадратів (матриць) для роз­вʼяза­н­ня ліній. рівнянь. «Чарівні квадрати» були ві­домі й давньоараб. математикам. При­близно тоді зʼявилося поня­т­тя принципу додава­н­ня матриць. Ви­значник матриці ввели япон. математик Т. Секі (1683) та нім. математик Ґ.-В. Лейбніц (1693). Після роз­витку теорії ви­значників швейцар. математик Ґ. Крамер почав роз­робляти свою теорію, а 1751 опублікував ві­доме правило Крамера. При­близно тоді ж нім. математик К.-Ф. Ґаус за­пропонував свій метод роз­­­вʼязува­н­ня систем ліній. рівнянь. Основу М. т. заклали в серед. 19 ст. ірланд. математик В.-Р. Гамільтон й англ. математик А. Келі. Фундам. результати належать нім. математикам К.-Т. Вейєрштрасу та Ф.-Ґ. Фробеніусу і франц. математику М.-Е. Жор­дану. Поня­т­тя «матриця», яке вже не було похідним від поня­т­тя «ви­значник», зʼявилося 1858 у праці А. Келі. Термін «матриця» першим почав вживати англ. математик Дж.-Дж. Сильвестр, який роз­глядав матрицю як обʼєкт, що породжує сімейство мінорів (ви­значників менших матриць, утворених викреслюва­н­ням рядків і стовпців з початк. матриці). К.-Ф. Ґаус першим встановив звʼязок між квадратич. формами, ліній. від­ображе­н­нями та матрицями. Франц. математик О.-Л. Коші роз­глядав ви­значники як многочлени та 1829 довів, що власні значе­н­ня симетр. матриць є дійс. числами. Багато теорем М. т. доводили спочатку для матриць малих роз­мірів: А. Келі теорему Гамільтона–Келі довів тільки для 2×2-матриць, а В.-Р. Гамільтон — для 4×4-матриць. Після цього властивостями ви­значників за­ймалися нім. учені Ф.-Ґ. Айзенштайн, К.-Ґ. Якобі, Л. Кронекер, К.-Т. Вейєрштрас, Ф.-Ґ. Фробеніус і В. Йор­дан.

Квадратні матриці за­стосовують для опису ліній. пере­творе­н­ня вектор. простору. Серед них окремо виділяють вироджені, невироджені, пере­ставні, подібні, конгруентні, нормал., унітарні, ортогонал., самоспряжені, симетр., косоерміт., кососиметр., додатньови­значені, проекційні, діагонал., одиничні, нульові. Окрім ви­значника, для квадрат. матриць важливою характеристикою є слід. За допомогою прямокут. матриць роз­вʼязують системи ліній. рівнянь. Для них важливими є такі поня­т­тя, як трикутна матриця, псевдообернена матриця, формула Ґревіля, сингуляр. роз­клад матриці, QR-роз­­­клад матриці та поляр. роз­клад матриці. Також для прямокут. матриць існує така важлива характеристика, як ранг. Під час ви­вче­н­ня блоч. матриць за­стосовують поня­т­тя: добуток Кронекера, оберне­н­ня блоч. матриці, матрична тотожність Вудбурі. Для аналіт. геометрії використовують матрицю повороту, матрицю пере­становки та матрицю Гаусголдера. У теорії графів виникає матриця інцидентності, матриця суміжності та степенева матриця; у цифр. оброблен­ні сигналів — бінарна матриця, матриця пере­становки та матриця Адамара. Матриці ві­ді­грають значну роль у теорії груп. За теоремою Машке ві­домо: нехай G — скінчен­на група та K — поле, характеристика якого не ділить порядок G, тоді груп. алгебра K[G] напів­проста; якщо характеристика поля K дорівнює 0, то K[G] є добутком матрич. алгебр над тілами над K; до­данки від­повід­ають незвід. зображе­н­ням G над K. За теоремою Бермана–Джонса ві­домо: нехай G — скінчен­на група; якщо для кожного простого p, яке ділить порядок G, p-силів. під­група G є циклічною порядку p, або p², тоді кількість неізоморф. нерозкладних ZG-модулів n(ZG) скінчен­на. Встановлено критерій скінчен­ності кількості нерозклад. зображень частково впорядков. множини над довіл. комутатив. кільцем. Пита­н­ня скінчен­ності цієї кількості можна звести до роз­вʼя­­за­н­ня матрич. задачі.

Засн. київ. школи з теорії зображень та теорії матрич. задач є А. Ройтер. За­пропонований ним лінійно-алгебраїч. метод дослідж., який роз­вивали його учні, до­зволив отримати низку важливих результатів у теорії зображень, зокрема щодо про­блем Бравера–Трол­ла та Ґабріеля для скінчен­но вимір. алгебр, задачі про опис скінчен­них p-груп із абелевою під­групою індексу p, задачі Гельфанда про модулі Гаріш-Чандри над алгеброю Лі групи SL(2, R). А. Ройтер, М. Клей­­нер і Л. Назарова довели критерій скінчен­ності для зображень скінчен­них частково впорядкованих множин; Ю. Дрозд довів ручну-дику дихотомію для широкого класу матрич. задач. Донині побудовано теорію зображень скінчен­них груп над полями. Матриці використовують під час побудови заг. ліній., діагонал., трикут., унітрикут., модуляр. груп. Скінчен­ну групу (зокрема й симетричну) можна точно зобразити матрицями пере­становок, що містять лише «0» та «1». Різноманітні про­блеми М. т. досліджують львів. учені М. Комарницький, Б. Забавський та їхні учні. Поле комплекс. чисел може бути точно зображене матрицями над полем дійс. чисел. При цьому комплекс. числу z = x + iy від­повід­ає матриця

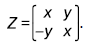
Тіло квартеніонів може бути точно зображене матрицями над полем дійс. чисел. При цьому елементу тіла кватерніонів q = t + ix + jy + kz від­повід­ає матриця

Літ.: Кэртис Ч., Райнер И. Теория пред­ставлений конечных групп и ас­со­­циативных алгебр / Пер. с англ. Мос­­ква, 1969; Мальцев А. И. Основы линейной алгебры. Москва, 1970; Назарова Л. А., Ройтер А. В. Пред­ставления частично упорядочен­ных множеств // Зап. науч. семинара Ленингр. отдел. Матем. ин-та. 1972. Т. 28; Воеводин В. В. Линейная алгебра. Москва, 1974; Курош А. Г. Курc высшей алгебры. Мос­­ква, 1975; Плахотник В. В. Пред­ставления частично упорядочен­ных множеств над ком­мутативными кольцами // Изв. АН СССР. Сер. матем. 1976. Т. 40, вып. 3; Кострикин А. И. Введение в ал­­гебру. Москва, 1977; Ван дер Варден Б. Л. Алгебра / Пер. с нем. Москва, 1979; Ланкастер П. Теория матриц / Пер. с англ. Москва, 1982; Y. A. Drozd, V. V. Kiri­­chenko. Finite Dimensional Algebras. Ber­­lin, 1994; P. Gabriel, A. Roiter. Representa­tions of Finite-Dimensional Algebras. Ber­­lin, 1997; Голуб Дж., ван Лоун Ч. Мат­­ричные вычисления / Пер. с англ. Мос­­ква, 1999; Гантмахер Ф. Р. Теория матриц. Москва, 2010.

В. В. Кириченко, М. В. Плахотник

Завантажити статтю