Математична модель
МАТЕМАТИ́ЧНА МОДЕ́ЛЬ
Наук. термін «модель» (від лат. modulus — міра, зразок) почали використовувати у 2-й пол. 19 ст. у своїх працях італ. математик Е. Бельтрамі, нім. математик Ф.-Х. Кляйн і франц. математик Ж.-А. Пуанкаре. Модель є матеріал. або уявним, тобто інформ., обʼєктом, що в процесі дослідж. заміщує обʼєкт-оригінал, при цьому маючи його істотні інформ. властивості. Вибір характеристик визначають відповідно до цілей моделювання. Процес абстрагування від несуттєвих параметрів називають формалізацією — заміною реал. обʼєкта або процесу формал. описом. М. м. — спеціал. метод, що дозволяє оцінити недоступні прямим вимірам властивості систем і процесів. Вона є системою матем. співвідношень, що всебічно описують обʼєкт дослідж., і джерелом нових відомостей, отриманих з їхньою допомогою. М. м. мають бути властиві адекватність, точність, універсальність, спроможність до визначення оцінок стійкості та чутливості. Вид М. м. залежить від природи реал. обʼєкта, завдань дослідж., необхід. достовірності та точності тощо. Донині створ. величезну кількість різноманіт. моделей. Рос. і амер. економіст, лауреат Нобелів. премії В. Леонтьєв на основі закону Вальраса розробив лінійну дискретно-детермінов. модель міжгалуз. балансу виробництва та розподілу продукції: Xi = ∑nj=1aijXj + yi , i = 1,—n, де Xi — валовий випуск продукції i галуззю; aij — коефіцієнт прямих витрат продукції i галузі на одиницю випуску j галуззю; Xj — валовий випуск продукції j галуззю; yi — кінцевий продукт i галузі. Модель відображає виробництво та розподіл сусп. продукту в галузі, міжгалуз. звʼязки, використання матеріал. і труд. ресурсів, створення та розподіл нац. доходу. Модель Мальтуса, що належить до неперервно-детермінов. моделей, — швидкість зростання популяції — диференц. рівняння xʼ = ax, де a — деякий параметр, що визначають різницею між народжуваністю та смертністю. Розвʼязком рівняння є експоненціал. функція x(t) = x0eat. Якщо a > 0 , то популяція необмежено, швидко зростає, але модель не враховує ресурси. На основі моделі Мальтуса побудовано модель хижак–жертва — розвиток двох антагоністич. популяцій (модель Лотки–Вольтерра)
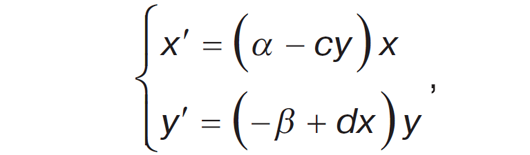
де x, y — відповідно кількість жертв і хижаків; a, b, c, d — коефіцієнти, що відображають взаємодії між видами. Поведінка системи є структурно нестійкою. Систему моделі гармоніч. осцилятора (або вільних коливань) представляють як масу, підвішену на закріпленій на одному кінці пружині. Її отримали на базі фундам. законів фізики (Ньютона та Гука), а описують ліній. диференц. рівнянням 2-го порядку m • x" + k • x = 0, де k — коефіцієнт пружності, m — маса тіла. Якщо врахувати фактори впливу на коефіцієнт пружності та представити його як k(x), то отримаємо нелінійну модель x: m • x" + k(x) • x = 0. Для моделей у частин. похідних незалеж. змінними є координати. Диференц. рівняння Лапласа
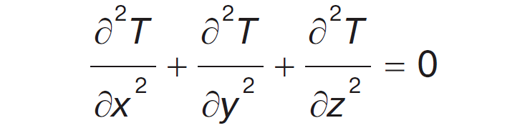
описує: розподіл електрич. потенціалу в області простору; стаціонар. розподіл температури в суціл. середовищі; потік ідеал. рідини. Система масового обслуговування (стохаст. модель) — матем. обʼєкт, що складається з приладів (каналів) обслуговування замовлень, що надходять у систему через накопичувач з утворення черги або без черги. Для систем із дискрет. станами та часом стаціонар. режим описують системою ліній. рівнянь: ∑n i=1,j≠1pi • pij = pj ∑ i=1,j≠1pji, ∑ni=1pi = 1; для систем з дискрет. станами та неперерв. часом — системою диференц. рівнянь Колмогорова:
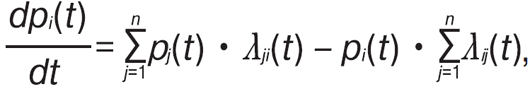
де pi — ймовірність перебування системи у стані; pij — перехідні ймовірності; lij — інтенсивність потоку із стану i в стан j.