Математичне сподівання

МАТЕМАТИ́ЧНЕ СПОДІВА́ННЯ – числова характеристика випадкової величини, що відповідає інтуїтивному поняттю її середнього значення. У зарубіж. літературі М. с. позначають літерою E (від лат. expectatio — очікування). У заг. випадку М. с. випадк. величини x з функцією розподілу Fx визначають рівністю Mx = ∫–∞+∞xdFx(x), якщо цей інтеграл, що розуміють в сенсі Лебеґа–Стіль-т’єса, існує. Еквівалент. чином М. с. випадк. величини можна означити як абстракт. інтеграл Лебеґа Mx = ∫Wx(w)P(dw), де W — множина елементар. подій, а P — ймовірнісна міра на цій множині. Якщо випадк. величина x приймає не більш ніж зчисленну кількість значень a1, a2, ... з ймовірностями p1, p2, ... відповідно, то її М. с. може бути обчислене за формулою Mx = ∑k≥1аkpk за умови, що цей ряд збігається абсолютно. Якщо ж випадк. величина x має щільність розподілу Px, то її М. с. представляють у вигляді Mx = ∫–∞+∞xpx(x)dx, де інтеграл розуміють в сенсі Лебеґа. М. с. зберігає властивості інтеграла. Зокрема, М. с. ліній. комбінації випадк. величин дорівнює відповід. ліній. комбінації їхніх М. с., а також для нього справджуються нерівності Гельдера та Мінковського. Дещо специфіч. властивостями М. с. є нерівності Чебишова та Ляпунова і те, що М. с. добутку незалеж. випадк. величин дорівнює добутку їхніх М. с. Якщо x — випадк. величина, а функція f: R → R є вимірною, то f(x) теж є випадк. величиною. При цьому формули 1–4 для обчислення М. с. f(x) набувають відповідно вигляду:

Mf(x) = ∫–∞+∞f(x)dFfx(x),

Mf(x) = ∫Wf(x(w))P(dw),

Mf(x) = ∑k≥1f(аk)pk,

Mf(x) = ∫–∞+∞f(x)px(x)dx.

Для натурал. числа n М. с. Mxn, M|x|n і M|x — Mx|n, якщо вони існують, називаються відповідно n-им моментом, n-им абсолют. моментом і n-им центрованим моментом випадк. величини x. При цьому 2-й центрований момент випадк. величини називають її дисперсією, а його квадрат. корінь — її середньоквадратич. відхиленням. Відповідність формал. означення інтуїтив. представленням може бути обґрунтовано посиленим законом великих чисел, згідно з яким середнє арифметичне результатів вимірювання величини при незалеж. експериментах збігається до М. с. цієї величини, тобто якщо x1, x2, ..., xn, ... — послідовність незалеж. однаково розподілених випадк. вели-чин зі скінченним М. с., то майже напевно має місце збіжність

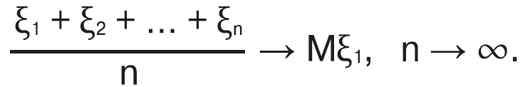
М. с. випадк. вектора (x1, x2, ..., xn) означається як матриця (Mx1, Mx2, ..., Mxn). У сучас. теорії ймовірностей поняття «М. с.» переносять і на випадк. елементи, що набувають значення у довіл. банах. просторі. В цьому випадку існує щонайменше 2 підходи, що базуються на інтегралах Петтіса (слабкий момент) та Бохнера (сильний момент).

Літ.: Колмогоров А. Н. Основные понятия теории вероятностей. Мос­ква; Ленинград, 1936; Гнеденко Б. В. Курс теории вероятностей. Мос­ква, 1967; Гихман И. И., Скороход А. В., Ядренко М. И. Теория вероятностей и математическая статистика. К., 1979; Вахания Н. Н., Тариеладзе В. И., Чобанян С. И. Вероятностные распределения в бана-ховых пространствах. Мос­ква, 1985; O. Kallenberg. Foundations of modern probability. 2002; Ширяев А. Н. Вероятность. Мос­ква, 2007. Т. 1–2.

А. А. Дороговцев, В. В. Фомічов

Рекомендована література

1. Колмогоров А. Н. Основные понятия теории вероятностей. Мос­ква; Ленинград, 1936;
   Google ScholarInternet
2. Гнеденко Б. В. Курс теории вероятностей. Мос­ква, 1967;
   Google ScholarInternet
3. Гихман И. И., Скороход А. В., Ядренко М. И. Теория вероятностей и математическая статистика. К., 1979;
   Google ScholarInternet
4. Вахания Н. Н., Тариеладзе В. И., Чобанян С. И. Вероятностные распределения в бана-ховых пространствах. Мос­ква, 1985;
   Google ScholarInternet
5. O. Kallenberg. Foundations of modern probability. 2002;
   Google ScholarInternet
6. Ширяев А. Н. Вероятность. Мос­ква, 2007. Т. 1–2.
   Google ScholarInternet

завантажити статтю