Кінематика

КІНЕМА́ТИКА (від грец. 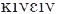 — рухатись)

у фізиці — роз­діл механіки, що ви­вчає способи опису руху матеріальних тіл без урахува­н­ня їхньої маси, діючих на них сил і причин виникне­н­ня руху. Окрім класич., або ньютонів. К., ви­окремлюють також релятивістську, яка ви­вчає способи опису рухів зі швидкостями, близькими до швидкості світла (див. Від­носності теорія). Рух обʼєктів мікросвіту (атомів, атом. ядер, елементар. частинок) досліджують методами квантової механіки. У класич. К. просторові (довжини від­різків) і часові (проміжки часу) характеристики руху вважаються абсолютними, тобто незалеж. від вибору системи від­ліку. В релятивіст. К. довжини від­різків і проміжки часу між двома подіями можуть змінюватися при пере­ході від однієї інерціал. системи від­ліку до іншої. Від­носною стає також одночасність. Класична К. є гранич. випадком релятивіст. К. Вихідні поня­т­тя К. — поня­т­тя простору та часу. У релятивіст. механіці замість окремих понять про­стір і час вводять поня­т­тя простору-часу, в якому інваріант від­носно пере­творень Лоренца — величина інтервалу. Про­стір і час є фіз. обʼєктами як і будь-які ін. матеріал. тіла, але набагато важливішими й істотнішими. Досліджуючи закони руху матеріал. тіл, ви­вчають властивості простору-часу. Залежно від властивостей досліджув. матеріал. тіла, що рухається, роз­різняють К.: матеріал. точки (матеріал. тіло, роз­мірами якого можна знехтувати порівняно з характер. від­станями між тілами), абсолютно твердого тіла (тіло, від­стань між двома будь-якими точками якого не змінюється, тобто воно не деформується), середовища, що деформується (пружно або пластично), та рідин і газів. Осн. задачі К.: ви­значе­н­ня положе­н­ня матеріал. тіла, що рухається, у будь-який момент часу (закону руху) та знаходже­н­ня кінемат. рівнянь руху — швидкості та при­скоре­н­ня з ви­значеними початк. умовами. Крім того, К. ви­вчає складні (складені) рухи матеріал. точки або абсолютно твердого тіла, тобто рухи, що здійснюються від­носно до декількох систем від­ліку, які взаємно пере­міщуються. Залежно від того, чи будуть функції координат, швидкості та при­скоре­н­ня за­дані аналітично, чисельно (таблицями) або графічно, для виріше­н­ня задач К. за­стосовують аналіт., чисел. або графічні методи. Матем. опис мех. руху в К. здійснюють за допомогою методів геометрії, алгебри, диференціал. та інтеграл. числе­н­ня, варіац. числе­н­ня, диференціал. геометрії тощо.

Тривалий час поня­т­тя про К. ґрунтувалися на працях давньогрец. мислителя Аристотеля (384–322 до н. е.), в яких стверджувалося, що швидкість паді­н­ня пропорційна вазі тіла, а рух при від­сутності сил неможливий. На­прикінці 16 ст. італ. учений Ґ. Ґалілей (1564–1642), ви­вчаючи вільне паді­н­ня (знамениті досліди на Пізан. вежі) й інерцію матеріал. тіл, довів неправильність ідей Аристотеля. Він же ввів поня­т­тя нерівномір. руху та при­скоре­н­ня матеріал. точки, сформулював закон інерції (принцип від­носності), який стосується властивостей інерціал. систем від­ліку. Італ. митець і вчений Леонардо да Вінчі (1452–1519) ви­вчав траєкторію тіл, кинутих під кутом до горизонту. Нім. астроном Й. Кеплер (1571–1630) від­крив 3 закони руху планет від­носно Сонця. Поміт. внесок у роз­виток К. зробили франц. філософ, математик, фізик, фізіолог Р. Декарт (1596–1650), який дослідив пита­н­ня про скла­да­н­ня довіл. числа рухів матеріал. точки, та нідерланд. вчений Х.-Х. Ґюйґенс (1596–1650), який роз­робив теорію коливань фіз. маятника. Франц. фахівець у галузі механіки та математик П. Варінь­йон (1654–1722), ви­ступаючи перед Франц. АН 20 січня 1700, вперше викори­став поня­т­тя швидкості та при­скоре­н­ня в диференціал. ви­гляді. Подальшим досягне­н­ням у К. слід вважати роботи швейцар. і рос. математика, фахівця у галузі механіки та фізика Л. Ейлера (1707–83), який роз­робив К. абсолютно твердого тіла та сформулював рівня­н­ня, що описують рух тіла навколо нерухомої точки, поклавши початок, зокрема, теорії гіро­скопів. У 18 ст. франц. фізик, математик і хімік А.-М. Ампер (1775–1836) першим викори­став варіац. числе­н­ня в К. Після створе­н­ня спец. теорії від­носності 1905 А. Айнштайном К. уві­йшла у новий етап роз­витку в рамках релятивіст. механіки.

Донині початк. зміст механіки — вче­н­ня про рух матеріал. точок і абсолютно твердих тіл з швидкостями, набагато меншими за швидкість світла, — значно роз­ширився. Серед ін. осн. понять К.: ступінь вільності абсолютно твердого тіла або системи матеріал. точок (кількість незалеж. параметрів — різних фіз. характеристик, зокрема координат, швидкостей, кутів, що одно­значно ви­значають стан і положе­н­ня абсолютно твердого тіла або системи матеріал. точок); мех. рух. (зміна взаєм. положе­н­ня матеріал. точки, матеріал. тіла або його частин у просторі від­носно ін. тіл протягом часу: напр., рух небес. тіл, рух літал. апаратів, рух машин і механізмів різного при­значе­н­ня, деформація елементів кон­струкцій і споруд, рух рідин і газів, коливал. рух матеріал. тіл, зокрема й колива­н­ня земної кори та водних мас під впливом Місяця тощо) — прямоліній., криволіній., коловий, по­ступал., рівно­при­скорений (рівносповільнений), нерівно­при­скорений, плоский тощо; кінемат. характеристики матеріал. точки — траєкторія, швидкість та при­скоре­н­ня; тіло від­ліку (тіло від­носно якого роз­глядається рух; мех. рух від­носний — рух одного і того ж тіла від­носно різних тіл виявляється різним); система від­ліку (утворюється тілом від­ліку або системою нерухомих один від­носно ін. тіл від­ліку, системою координат, що повʼязана з тілом від­ліку, та синхронізов. між собою годин­никами, які можуть бути роз­таш. в будь-якій точці простору, повʼязаній із системою від­ліку) — рухома та нерухома, інерціал. та неінерціальна; система координат (спосіб ви­значе­н­ня положе­н­ня матеріал. точки за допомогою чисел або ін. символів; введе­н­ня від­повід. системи координат означає введе­н­ня системи домовленостей про спосіб на­да­н­ня «адреси» кожній точці системи від­ліку; кожна точка системи від­ліку має свою, від­мін­ну від інших «адресу», а кожній «адресі» від­повід­ає лише одна точка системи від­ліку; система координат є матем. абстракцією, а систему від­ліку утворюють реал. тіла).

К. матеріал. точки. Існують вектор., координат. і природ. (за допомогою параметрів траєкторії) способи опису руху матеріал. точки. При вектор. способі положе­н­ня матеріал. точки в про-сторі від­носно деякої заздалегідь фіксов. точки — початку координат задають радіус-вектором 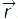. При русі матеріал. точки з положе­н­ня 1 в положе­н­ня 2 (рис. 1) її радіус-вектор змінюється в заг. ви­гляді як за модулем, так і за напрямком, тобто радіус-вектор 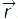залежить від часу t.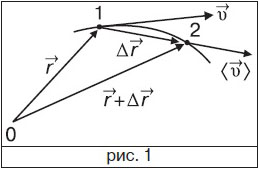
Геом. місце кінців радіус-вектора, що описує положе­н­ня матеріал. точки у просторі, називають траєкторією (фактично, це неперервна лінія, яку описує матеріал. точка при своєму русі у просторі). Рівня­н­ня траєкторії, напр., для плоского руху має ви­гляд y(x). Вектор пере­міще­н­ня 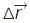характеризує пере­міще­н­ня радіус-вектора 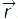за час ∆t. Від­ноше­н­ня 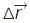/∆t називають серед. вектором швидкості 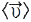за час ∆t. Вектор 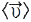збігається з напрямком вектора 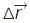. Мит­тєва швидкість матеріал. точки 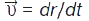направлена по дотичній до траєкторії у даній точці в сторону руху матеріал. точки (як і вектор 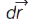). Рух матеріал. точки характеризується також при­скоре­н­ням: 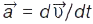. Напрямок вектора 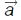збігається з напрямком вектора  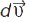— приростом вектора 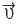за час 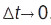. Прямою задачею К. є знаходже­н­ня швидкості 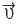та при­скоре­н­ня 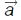матеріал. точки в будь-який момент часу за ві­домою залежністю 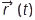. Зворотна задача К. 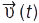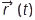полягає у знаходжен­ні і за ві­домою залежністю 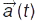. Для одно­знач. виріше­н­ня цієї задачі однієї залежності 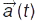недо­статньо, необхідно ще знати початкові, а саме швидкість 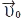і радіус-вектор 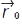матеріал. точки в деякий момент часу . Годо­графом вектора називають криву, яку описує кінець цього вектора з часом, якщо його початок весь час знаходиться в одній точці. Напр., годо­графом радіуса-вектора є траєкторія матеріал. точки, годо­графом вектора швидкості — крива, дотична до якої ви­значає напрямок вектора при­скоре­н­ня в цій точці. Рух матеріал. точки по колу описують залежністю 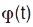, а кінемат. 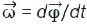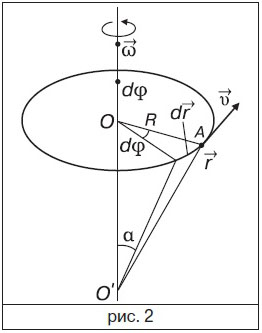характеристиками руху є мит­тєва кутова швидкість та мит­тєве кутове при­скоре­н­ня 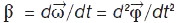(рис. 2). Лінійна та кутова швидкості матеріал. 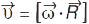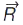точки повʼязані між собою спів­від­ноше­н­ням , де  — радіус-вектор, що проведений від центра кривини траєкторії до точки траєкторії, де роз­таш. у даний момент часу матеріал. точка.

Координат. спосіб ґрунтується на тому, що матеріал. точку жорстко привʼязують до від­повід. системи координат — декартової, циліндричної, сферичної тощо. Вибір тієї чи ін. системи координат ви­значається характером або симетрією задачі, а також намага­н­ням спростити роз­вʼязок задачі. При декарт. системі координат положе­н­ня матеріал. точки у просторі задається координатами 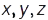. Знаючи закон руху матеріал. точки 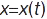; ; 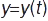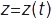, можна зна­йти проекції вектора 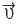швидкості на осі координат: 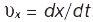; ; 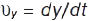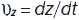. Модуль вектора швидкості

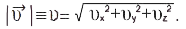
Напрямок вектора 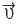задається напрямляючими косинусами за формулами 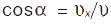; ; 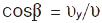, де , ,  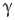— кути між вектором 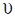та осями 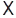, , 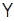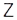від­повід­но. Скалярна середня швидкість матеріал. точки за час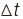

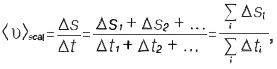
де 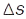 — увесь пройдений матеріал. точкою шлях;  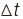— час, за який матеріал. точка проходить шлях 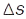;  — довжина ділянки шляху, яку матеріал. точка проходить за час 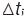. Шлях, пройдений матеріал. точкою, швидкість якої змінюється із часом за законом 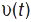, за проміжок часу від 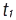до 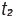, дорівнює

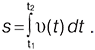
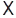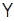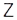
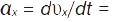
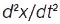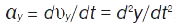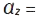
Проекції при­скоре­н­ня матеріал. точки на осі , , ; ; . Опис руху за допомогою параметрів траєкторії (природ. спосіб) за­стосовують тоді, коли траєкторія матеріал. точки ві­дома. Положе­н­ня матеріал. точки ви­значають дуговою координатою 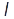 — від­стан­ню вздовж траєкторії від обраного початку від­ліку O (рис. 3).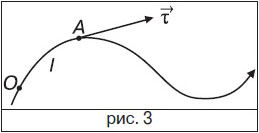
При цьому довільно обирають додат. напрямок від­ліку координати 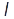. Закон руху матеріал. точки за­даний залежністю 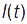. Одинич. вектор 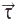, дотичний до траєкторії в довіл. точці A, збігається з напрямом вектора швидкості 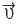. Вектор  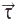— змін­ний вектор, він залежить від координати 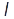. Тоді 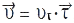, де 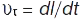 — проекція вектора 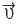на напрямок вектора 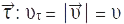. При­скоре­н­ня матеріал. точки

де 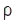радіус кривини траєкторії в даній точці: 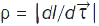, причому при 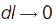виконується умова 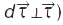;  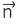— одинич. вектор нормалі до траєкторії, направлений до центра кривини: 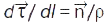. Модуль повного при­скоре­н­ня МТ

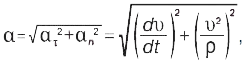
де 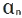,  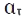— нормал. та тангенціал. компоненти при­скоре­н­ня.

Рух абсолютно твердого тіла. Най­простішими є по­ступал. і обертал. рухи абсолютно твердого тіла навколо нерухомої (закріпленої) осі. При по­ступал. русі всі точки абсолютно твердого тіла рухаються однаково та для зав­да­н­ня його руху до­статньо задати рух будь-якої однієї точки. Отже, по­ступал. рух абсолютно твердого тіла задається так само як і рух матеріал. точки. При обертал. русі навколо нерухомої осі тіло має одну ступінь вільності, його положе­н­ня ви­значається кутом повороту 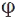і закон цього руху задається рівня­н­ням 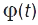. Кінемат. характеристики руху — кутові швидкість 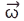і при­скоре­н­ня 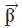тіла. Складнішим випадком обертал. руху є рух абсолютно твердого тіла, коли воно закріплене в одній точці (тіло має одну нерухому точку). Прикладом такого руху може служити рух гіро­скопа. У цьому випадку тіло має 3 ступеня вільності. Рух тіла біля нерухомої точки складається із елементар. поворотів навколо мит­тєвих осей оберта­н­ня, що проходять через цю точку. Осн. кінемат. характеристики руху: вектор мит­тєвої кутової швидкості, спрямов. по мит­тєвій осі оберта­н­ня, і вектор мит­тєвого кутового при­скоре­н­ня, спрямов. паралельно дотичній до кривої, описуваної кінцем вектора 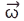. У заг. випадку вільне абсолютне тверде тіло має 6 ступенів вільності, а його рух описується 6-ма рівня­н­нями у ви­гляді перших похідних по часу від координат 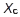, , 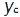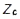полюса будь якої точки С тіла (за­звичай, центра мас тіла) та від кутів Ейлера, що ви­значають положе­н­ня тіла від­носно до осей, які пере­міщуються по­ступально разом з точкою С. Рух вільного абсолютно твердого тіла складається з по­ступал. руху тіла разом з полюсом С і елементар. поворотів навколо мит­тєвих осей оберта­н­ня, що проходять через цей полюс. Кінемат. характеристиками руху служать по­ступал. швидкість і по­ступал. при­скоре­н­ня, рівні швидкості і при­скорен­ню полюса, а також мит­тєва кутова швидкість і мит­тєве кутове при­скоре­н­ня руху тіла навколо полюса.

Складним, або складовим рухом матеріал. точки та абсолютно твердого тіла називається рух, що від­бувається одночасно від­носно до двох і більше систем від­ліку, одна з яких (К — СВ) вважається нерухомою, а інша (К′ — СВ) рухається від­носно першої. Рух, що здійснюється при цьому матеріал. точкою або твердим тілом від­носно до К′ — СВ, називається від­носним. Рух самої К′ — СВ і всіх повʼязаних з нею матеріал. точок і тіл від­носно до К — СВ є для рухомої точки (тіла) пере­носним. Рух матеріал. точки або твердого тіла від­носно до К — СВ називається абсолютним. Абсолютна швидкість 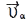матеріал. точки, що здійснює склад. рух, дорівнює геом. сумі від­носної 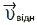і пере­носної 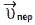швидкостей: 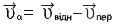. Від­повід­но: 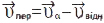. Абсолютне при­скоре­н­ня 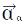в такому простому ви­гляді не подається: у К′ — СВ, що обертається, при пере­ході з однієї точки системи координат в іншу змінюється пере­носна швидкість матеріал. точки. Тому, якщо навіть 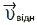при русі матеріал. точки не змінюється, вона повин­на за­знавати при­скоре­н­ня, від­мін­ного від пере­носного. Ось чому для К′ — СВ, що обертається, абсолютне при­скоре­н­ня 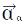дорівнює геом. сумі трьох при­скорень: від­носного 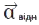, пере­носного 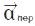і при­скоре­н­ня, яке називається при­скоре­н­ням Коріоліса 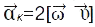. Остан­нє зумовлене рухом матеріал. точки від­носно неінерціальної К′ — СВ, що обертається.

При склад. русі абсолютно твердого тіла, коли його складові рухи є по­ступал., абсолют. рух тіла також буде по­ступал. зі швидкістю 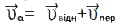. Якщо складові руху абсолютно твердого тіла обертальні навколо двох мит­тєвих осей оберта­н­ня, які пере­тинаються або паралельні, але 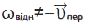, то результуючий рух буде також обертальним з кутовою швидкістю 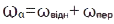. Якщо складовими рухами абсолютно твердого тіла є оберта­н­ня навколо деякої осі та по­ступал. рух у напрямку, паралельному цій осі, то результуючим рухом тіла є гвинт. рух.

К. рідини — роз­діл гідродинаміки, який ви­вчає лише геом. властивості руху рідини, незалежно від того, роз­глядається вʼязка або невʼязка рідина. К. рідини базується на властивості неперервності течії рідини, з якої випливає неперервність зміни кінемат. параметрів (швидкостей, при­скорень). Тобто швидкість рідини перед­бачається неперерв. функцією від координат, а отже такою, яку можна диференціювати. При дослідж. К. рідини її обʼєм пред­ставляють складеним із великої кількості частинок рідини. Існують 2 осн. методи дослідж. К. рідини: метод Лаґранжа і метод Ейлера. Найрозпо­всюдженішим є метод Ейлера, за яким роз­глядається поле швидкостей у різних точках течії.

Нині результати дослідж. в К. використовують як допоміжні при роз­вʼязуван­ні задач динаміки. К. стала основою для створе­н­ня багатьох приклад. напрямів: гі­дромеханіки, механіки деформов. твердого тіла, теорії коливань, гіро­скопії, теорії автомат. керува­н­ня, теорії польоту, навігації та ін. Крім того, методи К. мають важливе значе­н­ня при роз­рахунках пере­дач склад. (складених) рухів у різноманіт. механізмах і машинах, при роз­рахунках у небес. механіці тощо. Роз­діл геоморфології — К. рельєфу — ви­вчає зміну взаєм. положе­н­ня точок земної поверх­ні в часі та русі, але незалежно від сил. Поширюються методи прямої К. та інверс. К., які повʼязані з «планува­н­ням руху» в роз­робках робототехніки, трьохвимір. графіки, анімац. компʼютер. ігор тощо.

Поміт. внесок у роз­виток К., як і механіки в цілому, зробили укр. вчені Д. Ґраве, О. Дин­ник, Г. Савін, С. Тимошенко, А. Коваленко, М. Кільчевський, Г. Писаренко. Пита­н­нями К. за­ймаються на кафедрах низки ВНЗів України та в ін­ститутах НАНУ: Механіки, Про­блем міцності, Гі­дромеханіки (усі — Київ), Фізико-механічному, Приклад. про­блем механіки і математики (обидва — Львів), Приклад. математики і механіки (Донецьк), Тех. механіки (Дні­пропетровськ). Серед укр. наук. журналів, в яких друкують праці з різних питань, повʼязаних з К., — «Кинематика и физика небесных тел», «Технічна механіка», «Прикладная механика», «Механика твердого тела».

Завантажити статтю