Мероморфна функція

МЕРОМО́РФНА ФУ́НКЦІЯ (від грец. μέρος — дріб і ὅλος — вид) — у комплексному аналізі голоморфна функція, визначена на відкритій підмножині D комплексної площини С за винятком ізольованої підмножини точок (полюсів цієї функції). В околі кожного з полюсів М. ф. має розклад у ряд Лорана. Будь-яку М. ф. на множині D можна задати як частку між двома голоморф. функціями (зі знаменником, що не дорівнює нулю), визначених на D; кожен полюс повинен співпадати з нулем знаменника. Отже, М. ф. — це відношення двох голоморф. функцій. Така функція буде голоморфною, окрім точок, де знаменник дробу перетворюється на нуль, а значення функції прямує до нескінченності. В алгебрич. сенсі сукупність всіх М. ф. M(D) в області D — це поле часток кільця голоморф. функцій на D відносно звичай. поточк. операцій з наступ. доозначенням функцій у множині усувних особливостей. Аналогічно встановлюють залежність між множиною рац. і цілих чисел. Кожна М. ф. f ∈ M(D) задає неперервне відображення f області D у сферу Рімана С⋃{∞} (одновимір. комплекс. проектив. простір), що є голоморф. відображенням відносно комплекс. структури. Вірне й обернене твердження: кожне голоморфне відображення f:D→С⋃{∞} задає М. ф. f на D. При цьому множина полюсів f співпадає з дискрет. множиною f–1(∞). Таким чином, М. ф. однієї комплекс. змінної можна ототожнити з голоморф. відображеннями в сферу Рімана. Осн. задачі теорії М. ф. — це питання існування та побудови М. ф. із заданими особливостями. Значне місце в цій теорії посідає теорія розподілу значень (теорія Неванліни), що вивчає розподіл коренів рівняння f(z) = f, а ∈ С⋃{∞} при підході до межі області. Оскільки полюси М. ф. ізольовані, то їх не може бути більше зліченної множини. Але множина полюсів може бути нескінченною

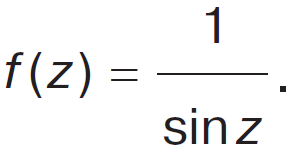
У випадку багатьох комплекс. змінних М. ф. задають локально як частку двох голоморф. функцій. Напр., f(z1, z2) = z1 / z2 є М. ф. на двовимір. комплекс. просторі. У багатовимір. випадку кожну М. ф. не можна розглядати як голоморфну функцію зі значеннями в сфері Рімана. Такі рац. функції, як

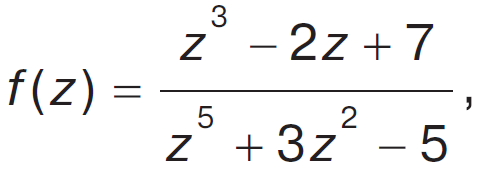
а також функції

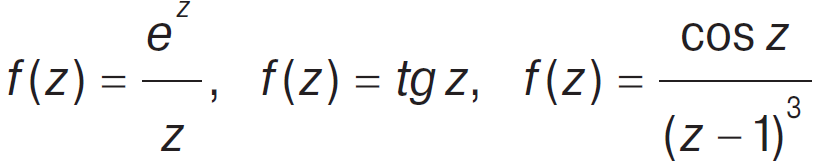
є мероморфними в усій комплекс. площині. Функція f(z) = задана на усій комплекс. площині за винятком початку координат z = 0. Але 0 не є полюсом цієї функції, а її особливою точкою. Отже, ця функція не є мероморфною в усій комплекс. площині. Але вона є мероморфною (навіть голоморфною) в С\{0}. Серед важливих М. ф. – гамма функція та дзета функція Рімана. Немероморфні функції: усі нерац. функції, напр. f(z) = z; усі функції, що мають логарифмічне розгалуження, напр., f(z) = ln(z). На Ріманових поверхнях кожна точка має відкритий окіл, що гомеоморфний відкритій множині комплекс. площини. Отже, поняття М. ф. може бути визначене для кожної Ріманової поверхні. На некомпакт. Рімановій поверхні кожна М. ф. може бути реалізована як частка двох (заданих глобально) голоморф. функцій. На компакт. Ріманових поверхнях кожне значення М. ф. приймають з однією частотою, а число нулів такої функції співпадає з числом її полюсів. М. ф. на еліптич. кривих називають еліптич. функціями. Осн. твердженнями в теорії М. ф. є теореми Вайєрштрасса, Міттаґ–Лефлера, про лишки та Рімана–Роха.

Розмір шрифту

Мероморфна функція

Рекомендована література

Інформація про статтю