Інтегральне числення
Визначення і загальна характеристика
ІНТЕГРА́ЛЬНЕ ЧИ́СЛЕННЯ — одна зі складових математичного аналізу, що вивчає інтеграли та їх застосування. Осн. поняття І. ч. — невизначений та визначений інтеграли. Метою диференціал. числення є знаходження похідної від заданої функції, але у багатьох випадках треба розвʼязувати обернену задачу — відшукання функції F(x), похідна F′(x) від якої збігається із заданою функцією f(x). Функція F(x) називається первісною для f(x). Вона існує не для всякої f(x). Але якщо f(x) неперервна на заданому відрізку, первісна функція існує завжди; більше того, таких функцій є нескінченна кількість. Множина всіх первіс. функцій для функції f(x) називається невизначеним інтегралом від f(x) і позначається символом ʃf(x)dx. Отже,
ʃf(x)dx = F(x) + C,
де C — довільна стала. Операція відшукання невизначеного інтеграла від заданої функції називається інтегруванням цієї функції і є дією, оберненою до диференціювання. Припустимо, що функція f(x) задана на відрізку [a, b]. Визначений інтеграл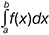 
від f(x) на [a, b] визначається як границя інтеграл. сум
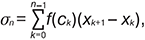
де ck — довільно вибрана точка з проміжку (xk, xk+1), a = x0 <x1 <... <xn = b — довільне розбиття інтервалу [a, b]. Якщо ця границя існує і не залежить від способу розбиття [a, b], то f(x) інтегрована на відрізку [a, b]. Звʼязок між невизначеним та визначеним інтегралами задається формулою Ньютона–Ляйбніца:
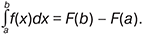
Визначений інтеграл застосовують для обчислення площ криволіній. фігур, швидкості руху за його прискоренням, моментів інерції, роботи сил тощо. Поняття визначеного інтеграла узагальн. з часом у звʼязку з необхідністю його застосування в різних напрямах. Так зʼявилися криволінійні, кратні, поверхн. інтеграли, інтеграли Рімана, Лебеґа, Бохнера, Данжуа та ін. Виникнення І. ч. повʼяз. переважно з обчисленням площ і обʼємів, в його основу покладено способи, які застосовували саме з цією метою Архімед та ін. античні математики. Важл. внесок у розвиток І. ч. зробили в 16–17 ст. Й. Кеплер, Б. Кавальєрі, Е. Торрічеллі, Б. Паскаль. І. Ньютон і Ґ.-Ф. Ляйбніц незалежно один від одного розробили для цих операцій системи позначень та правил, зʼясували у заг. формі звʼязок між ними й виділили їх у самост. розділ математики, засади якого широко застосовують у механіці. Подальший розвиток І. ч. повʼяз. з іменами І. Бернуллі, Л. Ейлера, О. Коші, Ґ. Рімана, Е. Бореля, А. Лебеґа, Ж. Ліувілля, П. Чебишева, Н. Лузіна та ін. Значний внесок в І. ч. для функцій багатьох змінних зробив М. Остроградський, імʼям котрого названо осн. формулу І. ч. — формулу інтегрування по частинах Остроградського–Ґаусса, яка є незамін. інструментом при дослідж. рівнянь матем. фізики.
Літ.: Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления: В 3 т. Москва, 1958–60; Кудрявцев Л. Д. Математический анализ. Москва, 1973; Давидов М. О. Курс математичного аналізу: У 3 ч. Ч. 1. К., 1976; Шкіль М. І. Математичний аналіз: У 2 ч. Ч. 1. К., 1978.
В. І. Горбачук
Додаткові відомості
Рекомендована література
Завантажити статтю
