Майже періодична функція

МА́ЙЖЕ ПЕРІОДИ́ЧНА ФУ́НКЦІЯ  — функція, значення якої при додаванні до аргументу належним чином вибраних сталих чисел (майже періодів) наближено повторюються. Існують різні способи означення класів М. п. ф., які базуються на поняттях майже періоду, замикання, зсуву тощо. Першу побудову неперерв. М. п. ф. запропонував данський математик Г. Бор (1923), який сформулював осн. властивості та довів теореми єдності й апроксимації. За Г. Бором, неперервна функція f(x), визначена для всіх дійс. значень x, називається М. п. ф., якщо для кожного числа ε > 0 можна вказати таке число l = l(ε) > 0, що в кожному інтервалі дійс. осі довжини l знайдеться хоча б одне таке число τ = τ(ε), що при будь-якому x виконується нерівність |f(x + τ) — f(x)| < ε. Числа τ називають майже періодами функції f(x). Період. функції є частк. випадками М. п. ф. Найпростіші приклади М. п. ф. можна отримати в результаті додавання періодич. функцій з неспіврозмір. періодами, напр. cos x + 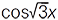. Найважливіші властивості: М. п. ф. обмежена та рівномірно неперервна на всій дійс. осі; сума та добуток скінченного числа М. п. ф. є М. п. ф.; границя рівномірно збіжної послідовності М. п. ф. є також М. п. ф.; теорема про середнє значення — для кожної М. п. ф. існує середнє на всій дійсній осі значення: 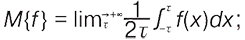кожній М. п. ф. можна поставити у відповідність ряд Фур’є: 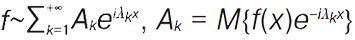(при цьому на відміну від періодич. функцій послідовність показників Фур’є 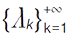може утворювати зчисленну множину, яка може бути всюди щільною); для кожної М. п. ф. має місце рівність Парсеваля: 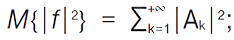теорема єдиності — якщо для даної М. п. ф. f всі її коефіцієнти Фур’є дорівнюють нулю, тобто, для всіх дійсних λ величина 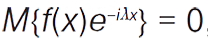, то f(x) ≡ 0, тобто ряд Фур’є однозначно визначає М. п. ф.; теорема апроксимації — для кожної М. п. ф. і кожного ε > 0 можна вказати такий тригономе­трич. поліном 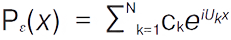, що при всіх дійсних x виконується нерівність 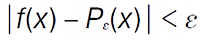(при цьому можна припускати, що показники U_k полінома P_ε вибира­ються із показників Фур’є функ­­ції f; навпаки, кожна функція f, яка володіє цією властивістю є М. п. ф.). До Г. Бора частк. випадок М. п. ф., зокрема т. зв. квазіперіод. функ­ції вивчали латв. математик П. Боль (1893) та франц. математик Е. Ескланьон (1904). Важливу роль у побудові теорії М. п. ф. відіграли результати укр. математика М. Боголюбова, який у своїх роботах розробив 2 різні методи доведення теореми апроксимації М. п. ф. Його дослідж. отримали широке визнання математиків всього світу та дали змогу поширити раніше відомі твердження для неперерв. М. п. ф. на більш широкі функціонал. класи. Узагальнення теорії М. п. ф. на розривні функції подав рос. математик В. Степанов (1925), а пізніше — нім. і амер. математик Г. Вейль та рос. і британ. математик А. Безикович. У дещо ін. напрямі відповідні дослідж. у теорії М. п. ф. провів укр. математик Б. Левітан.

Завантажити статтю