Квантова хромодинаміка

Визначення і загальна характеристика

КВА́НТОВА ХРОМОДИНА́МІКА — неабелева квантова теорія кольорових кварків — фундаментальних складових гадрон­ної матерії, та глюонів — квантів калібрувального векторного поля, що пере­носить між­кваркові взаємодії. К. х. побудована за зразком квантової електродинаміки на під­ставі принципу локал. калібрувал. інваріантності від­носно пере­творень у триколір. комплекс. просторі внутр. симетрій. Від­повід­но до сучас. уявлень, К. х. складає основу для опису сильної взаємодії між гадронами та від­повід­ає за сили, які звʼязують кварки в гадрони. К. х. виникла на поч. 1970-х рр. у результаті майже 10-річного процесу еволюції та синтезу уявле­н­ня про колір кварків, партон. картини глибоко непруж. взаємодії та апарату неабелевих калібрувал. полів. Початок цього процесу повʼязують із за­пропонованою в серед. 1960-х рр. амер. фізиками М. Ґелл-Ман­ном і Дж. Цвейґом (незалежно один від одного) гіпотезою кварків — суб­структур. частинок, із яких складаються всі гадрони. Нині ві­домо бл. 400 гадронів, які звʼязані станами: або пари кварк-антикварк (мезони), або трьох кварків (баріони), або трьох антикварків (антибаріони). Гадронів з ін. складом із кварків і антикварків поки що не виявлено, хоча теорія допускає існува­н­ня і деяких ін. кварк. структур. Кварки прийнято по­значати літерою q, антикварки — q, отже спо­стережувані гадрони мають одну з можливих структур: qq (мезони), qqq (баріони) і q q q (антибаріони). Вважається, що в природі існує шість різних типів або ароматів кварків q, які по­значають символами u, d, s, c, b, t, причому з них перші пʼять кварків уже від­криті екс­периментально в складі гадронів, а шостий кварк t є поки що гіпотетичним, але сучасна теорія елементар. частинок і деякі екс­перименти, напр., колаборації CDF та DO на колайдері Теватрон у Нац. при­скорювал. лаб. ім. Е. Фермі («Фермілаб»; м. Батавія, шт. Огайо, США, 1995), доводять і його існува­н­ня. Всі кварки є ферміонами, мають спін J = ½. Їхній дробовий баріон. заряд B = ⅓. Дробовий електрич. заряд Q для кварків u, c, t дорівнює ⅔, а для кварків d, s, b — –⅓ (в одиницях заряду протона або позитрона). Кварки u та d, як і обидва нуклони (протони і нейтрони), мають ізотопіч. спін (ізо­спін) Т = ½. Для кварка u проекція ізотопіч. спіну М_Т = +½, а для кварка d — М_Т = –½. Отже, кварки u та d утворюють ізотопіч. дублет, як протон і нейтрон. Ін. кварки ізотопіч. спіну не мають, але для кожного з них характерні специфічні нові заряди (або квант. числа). Заряд кварка s (т. зв. кварк дивність) S = –1, кварка c (чарівність) — С = +1, кварка b (краса) — B′ = –1. Недо­статньо ви­вчений кварк t (правдивість) повинен мати заряд Т′′ = +1. Як і у гадронів, заряди кварків повʼязані з проекцією ізо­спіну М_Т формулою Ґелл-Ман­на–Нішиджими: Q = М_Т + 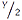, Y = B + S + C + B′ + Т′′, де Y — т. зв. гіперзаряд. Існують баріони, що складаються із кварків одного і того самого аромату, напр., ∆⁺⁺ = uuu та ∆^– = ddd. Спін цих двох гадронів 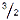, тобто спіни всіх трьох кварків у кожному з цих гадронів паралельні. Трапляються гадрони з однаковим складом кварків, але з різними властивостями. Напр., протон p = uud і дельта-частинка ∆⁺ = uud, яка має спін J = 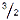та ізо­спін Т = 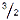. Гіперони Λ = uds і Σ⁰ = uds, які складаються із кварків u, d і s, мають навіть однаковий спін ½, але ізо­спін у Λ-частинки Т = 0, а у Σ⁰-частинки — Т = 1. Від­різняються Λ- і Σ⁰-гіперони і значе­н­ням маси. У всіх за­значених вище гадронів від­нос. орбітал. момент кварків дорівнює нулю. Але тоді для таких гадронів, як ∆⁺⁺, ∆^–, мав би порушуватися принцип Паулі, оскільки кварки під­порядковуються статистиці Фермі–Дірака. У звʼязку із за­значеною суперечністю між принципом Паулі та правилами скла­да­н­ня кварків у баріони амер. фізик О. Ґрінберґ 1964 за­пропонував використовувати для кварків парафермі-статистику порядку p = 3. Ця гіпотеза до­зволила пояснити властивість повної симетрії спін-унітар. хвильової функції баріонів, що сприяло можливості роз­ташувати до трьох спінових кварк. станів на одному й тому ж квант. рівні. Проте послідовне роз­вʼяза­н­ня про­блеми статистики кварків 1965 подали вітчизн. фізики М. Боголюбов, Б. Струмінський і А. Тавхелідзе та незалежно від них амер. фізик М. Хан і япон. фізик Ю. Намбу. Вони за­пропонували для кварків нове квант. число, згодом на­зване кольором (color). Ідею про те, що кварки повин­ні володіти додатк. квант. числом, вперше висловив Б. Струмінський у звʼязку з дослідже­н­ням магніт. моменту Ω^–-гіперона, складеного з трьох дивних кварків s з паралел. спінами. Квант. число кольору кварка С може мати три різні значе­н­ня, або три різні кольори, які умовно на­звали червоним (r), синім (b) і жовтим (y) за аналогією з трьома осн. кольорами видимого спектра. Змішува­н­ня реал. трьох таких кольорів призводить, як ві­домо, до білого кольору, тобто до від­сутності кольору. Не­звичність квант. числа кольору С полягає в тому, що колір. ступінь вільності (або просто колір) від­сутній у всіх спо­стережуваних частинок — гадронів. У реал. гадронах, як в баріонах, так і в мезонах, кольори кварків (антикварків), що входять до їхнього складу, взаємно компенсуються. Отже, від­носно до нового квант. числа-кольору всі фізично спо­стережувані гадрони виявляються нейтральними (або «без­кольоровими», С = 0). У випадку мезона кварк та антикварк, що входять до його складу, мають доповнювальні один до одного кольори (колір та антиколір), які при змішуван­ні й призводять до без­колір. мезона. Введе­н­ня кольор. кварків як фундам. частинок, які під­порядковані статистиці Фермі–Дірака, до­зволило роз­вʼязати низку фундам. про­блем теорії елементар. частинок, а поня­т­тя «кольору» лягло в основу К. х. — калібрувал. теорії сильних взаємодій (Ю. Намбу,1966), на якій ґрунтується гіпотеза про полон кварків (і антикварків) у гадронах. Це явище ще називають конфайнментом, або утрима­н­ням кварків у гадронах. Не­зважаючи на те, що існува­н­ня кварків доведено, від­ділити будь-який один кварк, тобто зафіксувати окремо, від довіл. гадрона, як електрон від атома чи нуклон від ядра, екс­периментально ще не вдавалося до цього часу. З цим повʼязані деякі не­звичні властивості сильної кварк-кваркової взаємодії. Вона під­силюється, коли від­стань між кварками зро­стає, і набирає на від­станях порядку гадрон. роз­мірів (~10^-13 см ≡ 1 фм) таке велике значе­н­ня, що кварки далі вже не можуть роз­ходитися. Знач. інтерес викликають майбутні спо­стереже­н­ня на споруджуваному ультрасучас. при­скорювал. комплексі у Центрі анти­протон. та іон­них досліджень (м. Дармштадт, Німеч­чина) високо­енергетич. жмутків анти­протонів і важких радіо­актив. ядер. Докладне ви­вче­н­ня в цих прецизій. екс­периментах екс­тремал. станів баріон. матерії та фазового пере­ходу до кварк-глюон. плазми стане важливим етапом у роз­вʼязан­ні про­блеми полоне­н­ня кварків у гадронах. Симетрій. основою К. х. слугує неабелева унітарна SU(3)_c, яка діє у тривимір. колір. просторі. Ця симетрія повʼязана з кольор. виродже­н­ням кварків: сильні взаємодії однакові для всіх кольор. кварків. Специфіка колір. станів — їхня не­спо­стережуваність на асимптотично великих простор. від­станях. Втім, усі спо­стережувані у дослідах мезони та баріони є синглетами кольор. групи SU(3)_c, тобто їхні вектори стану не змінюються при пере­творе­н­нях у колір. просторі. За своєю структурою К. х. подібна до квант. електродинаміки, але має і сут­тєві від­мін­ності. Як у квант. електродинаміці електрич. заряд унаслідок калібрувал. симетрії породжує електромагнітне поле, так кольор. кварки у К. х. породжують вісім різновидів кольор. глюон. полів — вектор. калібрувал. полів Янґа–Міл­лса. Оскільки глюон­ні поля, на від­міну від електромагнітного, несуть кольор. заряд, вони самі породжують ін. глюон­ні поля, з якими взаємодіють. Внаслідок цього рівня­н­ня для глюон. полів (на від­міну від рівнянь Максвел­ла у вакуумі) є нелінійними. Квантами глюон. калібрувал. поля є вісім різних глюонів, які мають, як і фотон, нульову масу спокою та спін, що дорівнює одиниці. Велика кількість різних глюонів пояснюється тим, що кожний глюон несе не один колір, як кварк, а від­разу два (колір і антиколір). При випускан­ні та по­глинан­ні глюонів кварки (і глюони) можуть змінювати свій колір, але не змінюють аромату. Наявність кольор. зарядів у глюонів зумовлює взаємодію між ними та призводить до того, що глюони, як і кварки, не можуть вилітати із гадронів. За­значені характерні особливості К. х. знаходять екс­перимент. під­твердже­н­ня в числен. вимірюва­н­нях жорстких процесів, а також у властивостях кварконіїв — звʼязаних станів важких кварків c, b, ... зі своїми антикварками (cc, bb, …). Важливий етап еволюції структур. моделей гадронів повʼязаний з уявле­н­ням про партони (за­пропонував 1966 амер. фізик Р.-Ф. Фейнман) — точк. квазівіл. складових гадронів. Це уявле­н­ня виникло із встановленої екс­периментально від­мін­ності у поведінці структур. функцій глибоко непруж. процесів і формфакторів пружного роз­сія­н­ня лептонів на гадронах, які вдається сумістити лише у припущен­ні про існува­н­ня точк. (слабовзаємодіючих) складових гадронів — партонів. Подальше екс­перимент. ви­вче­н­ня жорстких процесів, в яких досліджували структуру гадрона на малих від­станях, показало, що він є склад. динаміч. системою із складовими частинами (партонами): валент. кварками та антикварками, глюонами, а також величез. кількістю віртуал. кварк-антикварк. пар, нейтральних за всіма зарядами. Оскільки про роз­міри кварків ві­домо тільки те, що вони набагато менші, ніж гадрони, то можна стверджувати, що гадрони порожні, як і атоми. Квантовопольове оформле­н­ня нових фіз. уявлень отримало роз­виток після того, як для неабелевих калібрувал. теорій був від­критий 1973 амер. фізиками Д. Ґрос­сом, Ф.-Е. Вілчеком і Г.-Д. Політцером (незалежно від двох попередніх) феномен асимптотич. свободи, який став ключовим у теор. описан­ні партон. картини на основі кварк-глюон. динаміки. Завдяки властивості асимптотич. свободи колірна кварк-глюон­на взаємодія немовби самовиключається зі зменше­н­ням від­стані, внаслідок чого в ультрафіолет. межі кварки та глюони поводяться як квазівільні (невзаємодіючі) точк. обʼєкти. На малих від­станях між кварками або при до­статньо великих їхніх від­нос. енергіях та імпульсах кон­станта звʼязку сильної взаємодії α_с (аналог сталої тонкої структури в квант. електродинаміці) дуже мала. Остан­нє пояснюється неліній. взаємодією глюонів, яка призводить до ефектив. антиекранува­н­ня кольор. заряду кварків (оточених хмарою віртуал. глюонів і кварк-антикварк. пар). Ця фіз. картина й знаходить природне теор. поясне­н­ня з допомогою властивості асимптотич. свободи. Квантовопольова модель, що описує взаємодію ферміон. кварк. полів за допомогою калібрувал. глюон. поля, яке виникає унаслідок локалізації кольор. SU(3) симетрії, отримала назву «К. х.». Від­мін. рисою К. х. є та об­ставина, що вона формулюється з допомогою кварк. і глюон. полів, кванти яких (тобто кварки і глюони) не спо­стерігаються у вільному стані. З огляду на це можна стверджувати, що фіз. під­ґрунтя К. х. містить фіз. абстракцію вищого рівня порівняно з квант. теоріями електромагніт. і слабких взаємодій. Більшість сучас. методів квантової теорії поля дієва при невеликих кон­стантах звʼязку, тобто у випадку К. х. — при до­статньо великих від­нос. енергіях та імпульсах кварків. Кварки обмінюються при цьому пере­важно одним віртуал. глюоном, і теоретично такий процес взаємодії можна описати теорією збурень. Тому роз­виток К. х. зосереджений у першу чергу в напрямі пертурбатив. роз­рахунків характеристик гадрон. процесів, повʼязаних із взаємодією кварків і глюонів на малих від­станях. Для того, щоб використовувати результати таких обчислень у фізиці гадронів, за­проваджують напів­феноменол. обʼєкти — хвильові та структурні функції гадронів, що описують їхній кварк-глюон. склад. Най­природнішою сферою за­стосува­н­ня теорії збурень К. х. є жорсткі процеси з участю гадронів, тобто високо­енергетичні процеси з великими пере­дачами імпульсу. Основу такого за­стосува­н­ня складають кварк-гадрон­на дуальність і ренормалізаційна інваріантність амплітуд та пере­різів фіз. процесів. Гіпотеза кварк-гадрон. дуальності полягає у тому, що будь-який без­колір. стан із за­даними квант. числами можна зобразити або як суперпозицію гадрон. станів, або як суперпозицію кварк-глюон. станів з тими ж квант. числами. Її за­стосовують у всіх сучас. напрямах К. х. Важливі результати отримали й укр. фізики. В. Шелест, Г. Зіновʼєв, В. Миранський, Л. Єнковський, М. Кобилінський побудували клас дуал. амплітуд з мандельштамів. аналітичністю для пруж. і непруж. процесів зі­ткнень гадронів; вперше показали їхню сумісність з умовою унітарності; довели, що за­пропонована модель описує широке коло екс­клюзив. та інклюзив., дифракцій. та недифракцій. гадрон. процесів, є прототипом теорії взаємодії струн. Викори­ста­н­ня результатів теорії збурень перед­бачає малу величину кон­станти звʼязку. Завдяки властивості асимптотич. свободи це можна очікувати лише на до­статньо малих від­станях. Та коли від­стані між кварками великі, тобто порівняні з гадрон. роз­мірами, кварки обмінюються багатьма глюонами, кон­станта звʼязку сильної взаємодії при цьому стає великою, і квантовохромодинам. теорію збурень вже не можна використовувати. Методами теорії збурень неможливо дослідити механізм конфайнменту, роз­рахувати спектр мас гадронів, характеристики їхньої низько­енергетич. взаємодії тощо. Для К. х. є над­звичайно важливим роз­виток квантовопольових методів, які не використовують малі взаємодії. Істотно доповнює метод теорії збурень під­хід, базований на зображен­ні квант. амплітуд у ви­гляді фейнманів. континуал. (або функціонал.) інтегралів. Він використовує на­ближені обчисле­н­ня методом Монте-Карло (випадк. проб) по­втор. інтегралів високої кратності, які апроксимують континуал. інтеграли. Цей, т. зв. ґратковий, варіант К. х. — модел. спроще­н­ня локал. К. х., яке отримують за допомогою низки на­ближень. Спочатку неперерв. 4-вимір. просторово-часовий многовид замінюють дис­крет. сукупністю точок {n} = {an₁, an₂, an₃, an₄,} з однаковим кроком по кожному з чотирьох вимірів. Ці точки можна роз­глядати як вузли ґратки. Функції неперерв. змін­них — поля — пере­творюються у функції дис­крет. змін­них. Всі похідні замінюють на скінчен­ні різниці, а інтеграли — на суми за вузлами. При цьому поля кварків задають у вузлах ґратки, а поля глюонів — на її ребрах. У сучас. обчисле­н­нях використовують ґратки скінчен. роз­мірів 32³ × 64, що мають 32 точки за кожною просторовою координатою та 64 точки за часом. Введе­н­ня ґратки зі скінчен. кроком призводить також до регуляризації ультрафіолет. роз­біжностей, повʼязаних з малими від­станями, тобто з локальністю взаємодії. Одним з перших знач. досягнень теорії поля на ґратці стало від­кри­т­тя того факту, що ґратк. теорія окрім симетрій і складу полів К. х. володіє також і конфайнментом. Доведено, що кулонів. потенціал взаємодії між двома статич. кварками зі збільше­н­ням від­стані замінюється зростаючим потенціалом, близьким до лінійного, що може забезпечити конфайнмент. Унаслідок цього можливий опис властивостей гадронів за допомогою потенціал. моделей. Так, напр., у працях укр. фізиків В. Лазура, О. Рейтія та В. Рубіша побудовано релятивіст. потенціал. модель змішаних мезонів (К. х. аналогів водневоподіб. атомів), у якій рух легкого кон­ституєнт. антикварка q (кварка q) описується рівня­н­ням Дірака зі скалярно-вектор. звʼязком, а важкий кварк q (антикварк q) роз­глядається як локал. джерело глюон. поля. У на­ближен­ні центр. сил феноменол. потенціал qq-взаємодії апроксимується комбінацією пертурбатив. (кулоноподіб.) потенціалу одноглюон. обміну та далекосяж. (лінійно зростаючих з від­стан­ню r) лоренц-скаляр. S_l,r(r) і лоренц-вектор. V_l,r(r) потенціалів. За допомогою роз­виненого апарату квазікласич. асимптотик для рівня­н­ня Дірака зі скалярно-вектор. звʼязком отримано зручні асимптотичні формули для енергетич. і масового спектрів, середніх радіусів і хвильових функцій важко-легких (D-, D_s-, В- і B_s-) мезонів, які забезпечують високу точність роз­рахунків навіть для станів з радіал. квант. числом n_r ~ 1. Встановлено, що конфайнмент кварків можна забезпечити лише у тих релятивіст. потенціал. моделях, в яких у далекосяж. частині потенціалу між­кварк. взаємодії від­носна вага лоренц-скаляра S_l,r(r) домінує над від­нос. вагою лоренц-вектора V_l,r(r). Теор. аналіз К. х. на ґратці показує, що при до­статньо високих густинах енергії повинен від­буватися фазовий пере­хід сильновзаємодіючої матерії до нового стану, на­званого кварк-глюон. плазмою, в якому кольор. кварки і глюони можуть рухатися вільно на великі від­стані порядку кількох фермі. Ще однією принципово важливою властивістю такого стану матерії є від­новле­н­ня в ньому кірал. симетрії, яка спонтан­но порушена в нормал. ядер. матерії, що веде до наявності у кварків ефектив. мас, значно більших (при­близно на 300 МеВ) за їх справжні (струмові) маси. Досліджен­ню властивостей сильновзаємодіючої матерії в екс­тремал. умовах (при високих т-рах і густинах) присвячені піонер. праці укр. вчених Г. Зіновʼєва, М. Горенштейна, О. Кобушкіна, О. Борисенка, С. Машкевича, В. Петрова, Ю. Синюкова, К. Бугаєва, Д. Анчишкіна та В. Скалозуба. Для знач. кількості ефектив. модел. гамільтоніанів вони за­пропонували нове роз­вʼяза­н­ня (від­сутнє в існуючих дослідже­н­нях) для динаміч. маси кварка як функції баріон. хім. потенціалу, що до­зволило продемонструвати від­сутність стрибка густини кварк. ансамблю, який свого часу був одним з найсут­тєвіших аргументів в об­ґрунтуван­ні екс­перимент. про­грами пошуку фазового пере­ходу від­новле­н­ня кірал. симетрії при високих т-рах та баріон. густинах. Ними наведено аргументи, що вірогід. сценарієм (часткового) від­новле­н­ня кірал. симетрії може бути наявність змішаної фази вакууму та баріон. матерії; ви­вчено деякі властивості крапель кварк. рідини, подібних в цілому до ядра. За­пропоновано (у низько­енергетич. зоні) і більш феноменологічні під­ходи. У більшості з них сут­тєво використовується поня­т­тя про кварк. та глюон­ні конденсати, які зумовлені нетривіал. структурою вакууму К. х., все ще недо­статньо зро­зумілою до цього часу. Вагомий внесок у роз­виток теорії сильної взаємодії зробили укр. дослідники Ю. Ломсадзе, В. Сабов, Ю. Ільїн: роз­робили методи побудови ефектив. лаґранжіанів, що ґрунтуються на динаміч. симетрії кірал. груп; без­посередньо із К. х. одержали низько­енергетич. ефектив. лаґранжіан, який призводить до нового типу роз­вʼязків неліній. рівнянь — солітонів; виконали теор. дослідж. нетривіал. характеристик вакууму К. х., який може бути заселений непертурбатив. флуктуаціями типу ін­стантонів, а також різними конденсатами. Низку важливих результатів одержали теоретики всесвітньо ві­домої наук. школи Л. Ландау й О. Ахієзера у галузі електродинаміки гадронів: у рамках динаміч. теорії полюсів Редже дослідили процеси фото- та електронародже­н­ня скаляр. і вектор. мезонів та дивних частинок на нуклонах (М. Рекало); роз­винули теорію поляризацій. явищ при взаємодії елементар. частинок (О. Ахієзер, М. Рекало, Ю. Куліш, Г. Гах, А. Рекало); дослідили процеси фото- та електророзщепле­н­ня гадронів, роз­паду частинок, комптонів. роз­сія­н­ня на нуклонах, реакції електрон­но-позитрон. анагіляції в гадрони, ефекти поруше­н­ня простор. парності у процесах електромагніт. взаємодії гадронів (М. Рекало, Г. Гах, А. Рекало, О. Корчин, С. Івашин, М. Меренков, О. Шеховцова, М. Кончатний, В. Ковальчук). Нині в Україні також успішно працюють та роз­виваються всесвітньо ві­домі наук. школи М. Боголюбова й О. Парасюка та П. Фоміна: В. Гусинін, Л. Єнковський, В. Миранський, Г. Зіновʼєв, М. Горенштейн, О. Кобушкін, О. Борисенко, С. Машкевич, В. Петров, Ю. Синюков, К. Бугаєв, Д. Анчишкін, О. Гаврилик, П. Голод, Ю. Ситенко та ін. Важливі результати, отримані пред­ставниками цих двох наук. шкіл, сприяють високому рівню та подальшому роз­витку К. х. та квант. теорії поля. Під­готовку фахівців з теор. фізики, зокрема К. х., здійснюють університети Києва, Харкова, Дні­пропетровська, Донецька, Львова, Ужгорода, Чернівців.

Літ.: M. Gell-Mann. Isotopic spin and new unstable particles // Phys. Rev. 1953. Vol. 92, № 3; K. Nishijima. Charge independence theory of V particles // Progress of Theoretical Physics. 1955. Vol. 13, № 3; M. Gell-Mann. A schematic model of baryons and mesons // Phys. Lett. 1964. Vol. 8, № 3; O. W. Greenberg. Spin and unitary-spin in dependence in a paraquark model of baryons and mesons // Phys. Rev. Lett. 1964. Vol. 13; M. Y. Han, Y. Nambu. Three-triplet model with double SU(3) symmetry // Phys. Rev. 1965. Vol. 139, № 4 B; Y. Nambu. A systematics of hadrons in subnuclear physics // Preludes in Theoretical Physics. Amsterdam, 1966; A. I. Bugrij, G. Cohen-Tannoudji, L. L. Jenkovsky, N. A. Kobylinsky. Dual amplitudes with Mandelstam analyticity // Fortschritte der Physics. 1973. Vol. 21; Шелест В. П., Зиновьев Г. М., Миранский В. А. Модели сильновзаимодействующих элементарных частиц. Москва, 1975. Т. 1; 1976. Т. 2; L. L. Jenkovsky, A. A. Trushevsky. Asymptotic of total cross-sections and ultimate temperature of hadronic systems // Nuovo Cimento A. 1976. Vol. 34; Индурайн Ф. Квантовая хромодинамика. Введение в теорию глюонов / Пер. с англ. Москва, 1986; Кройц М. Кварки, глюоны и решетки. Москва, 1987; Боголюбов Н. Н., Логунов А. А., Оксак А. И., Тодоров И. Т. Общие принципы квантовой теории поля. Москва, 1987; Ситенко О. Г., Тартаковський В. К. Теорія ядра. К., 2000; Лазур В. Ю., Рейтий А. К., Рубиш В. В. Метод ВКБ для уравнения Дирака со скалярно-векторной связью // ТМФ. 2005. Т. 143, № 1; Вони ж. Квазикласcическое при­ближение в релятивистской потенциальной модели В- и D-мезонов // Там само. 2008. Т. 155, № 3; Вони ж. Quasiclassical theory of the Dirac equation with a scalar-vector interaction and its applications in the physics of heavy-light mesons // Phys. Rev. D. 2011. Vol. 83, № 7; K. Aamodt, G. M. Zinovjev. Centrality dependence of the charged-particle multiplicity density at mid-rapidity in Pb-Pb collisions at sqrt (S-NN) = 2.78 TeV // Phys. Rev. Lett. 2011. Vol. 106; Красников Н. В., Матвеев В. А. Новая физика на Большом адрон­ном кол­лайдере. Москва, 2011; Фортов В. Е., Шарков Б. Ю., Штокер Х. На­учная про­грам­ма в новом международном центре фундаментальной физики — Европейском центре анти­протон­ных и ион­ных ис­следований FAIR // УФН. 2012. № 6.

В. Ю. Лазур

Завантажити статтю